Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью )
либо интеграл на замену переменной (см. статью )
либо интеграл как раз на метод интегрирования по частям
.
Как всегда, под рукой должны быть: Таблица интегралов
и Таблица производных
. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы
. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение
функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы: . Зато есть такая:  – формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).
И сразу список в студию. По частям берутся интегралы следующих видов:
1) ,  , – логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) , – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.
3) ,  , – тригонометрические функции, умноженные на какой-нибудь многочлен.
4) , – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям: 
Формула применяется слева направо
Смотрим на левую часть: . Очевидно, что в нашем примере (и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за , а что-то за .
В интегралах рассматриваемого типа за всегда обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за мы обозначили логарифм, а за – оставшуюся часть
подынтегрального выражения.
Следующий этап: находим дифференциал :
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию . Для того чтобы найти функцию необходимо проинтегрировать правую часть
нижнего равенства :
Теперь открываем наше решение и конструируем правую часть формулы: .
Вот кстати, и образец чистового решения с небольшими пометками:
Единственный момент, в произведении я сразу переставил местами и , так как множитель принято записывать перед логарифмом.
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после
применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения:  . И это не случайно.
Формула интегрирования по частям  и формула  – это два взаимно обратных правила.
Пример 2
Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже говорилось, за необходимо обозначить логарифм (то, что он в степени – значения не имеет). За обозначаем оставшуюся часть
подынтегрального выражения.
Записываем в столбик:
Сначала находим дифференциал :
Здесь использовано правило дифференцирования сложной функции  . Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений
я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.
Теперь находим функцию , для этого интегрируем правую часть
нижнего равенства :
Для интегрирования мы применили простейшую табличную формулу 
Теперь всё готово для применения формулы  . Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью :
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за в похожих ситуациях всегда обозначается логарифм.
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей
скобке  , и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3
Найти неопределенный интеграл.
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Пример 4
Найти неопределенный интеграл.
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3,4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т.д. Нет, конечно, презерватив на глобус
я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции
=).
Интегралы от экспоненты, умноженной на многочлен
Общее правило:
Пример 5
Найти неопределенный интеграл.
Используя знакомый алгоритм, интегрируем по частям:
Если возникли трудности с интегралом , то следует вернуться к статье Метод замены переменной в неопределенном интеграле
.
Единственное, что еще можно сделать, это «причесать» ответ:
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом  или даже 
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что – сложная функция.
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
Интегрируем по частям:
Хммм, …и комментировать нечего.
Пример 8
Найти неопределенный интеграл
Это пример для самостоятельного решения
Пример 9
Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за обозначается многочлен.
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла , то рекомендую посетить урок Интегралы от тригонометрических функций
.
Пример 10
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»…. Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за всегда обозначается обратная тригонометрическая функция
.
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками» |
Определённым интегралом
от непрерывной функции f
(x
) на конечном отрезке [a
, b
] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом
(Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F
(b
) - F
(a
)).
Числа a
и b
называются соответственно нижним и верхним пределами интегрирования, а отрезок [a
, b
] – отрезком интегрирования.
Таким образом, если F
(x
) – какая-нибудь первообразная функция для f
(x
), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница
. Разность F
(b
) – F
(a
) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F
(x
) и Ф(х
) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х
) = F
(x
) + C
. Поэтому
Тем самым установлено, что на отрезке [a
, b
] приращения всех первообразных функции f
(x
) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная
С
из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела
b
, далее - значение
нижнего предела
a
и вычисляется разность
F(b) - F(a)
. Полученное число и будет
определённым интегралом.
.
При a
= b
по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С
= 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2.
Вычислить определённый интеграл
Решение. Используя формулу
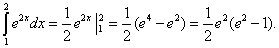
Свойства определённого интеграла
Теорема 2.
Величина определённого интеграла не зависит от обозначения переменной интегрирования
, т.е.
(40)
Пусть F
(x
) – первообразная для f
(x
). Для f
(t
) первообразной служит та же функция F
(t
), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3.
Постоянный множитель можно выносить за знак определённого интеграла
, т.е.
(41)
Теорема 4.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций
, т.е.
(42)
Теорема 5.
Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям
, т.е. если
(43)
Теорема 6.
При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак
, т.е.
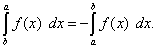(44)
Теорема 7
(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его
, т.е.
(45)
Теорема 8.
Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9.
Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать
, т.е.
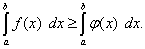(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5.
Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f
(x
) – непрерывная на отрезке [a
, b
] функция, а F
(x
) – её первообразная. Рассмотрим определённый интеграл
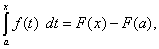(47)
а через t
обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х
меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х
, которую обозначим через Ф
(х
), т.е.
(48)
Докажем, что функция Ф
(х
) является первообразной для f
(x
) = f
(t
). Действительно, дифференцируя Ф
(х
), получим
так как F
(x
) – первообразная для f
(x
), а F
(a
) – постояная величина.
Функция Ф
(х
) – одна из бесконечного множества первообразных для f
(x
), а именно та, которая при x
= a
обращается в нуль. Это утверждение получается, если в равенстве (48) положить x
= a
и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F
(x
) – первообразная для f
(x
). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции
, равна
Пусть α и β – значения переменной t
, при которых функция
принимает соответственно значения a
и b
, т.е.
Но, согласно формуле Ньютона-Лейбница, разность F
(b
) – F
(a
) есть
Понятие первообразной и неопределенного интеграла. Теорема о совокупности первообразных. Свойства неопределенного интеграла. Таблица интегралов.
Функция F(x) называется первообразной для функции f(x) , на заданном промежутке, если на этом промежутке функция F(x) непрерывна, и в каждой внутренней точке промежутка справедливо равенство: F’(x) = f(x)
Теорема 1
. Если функция F(x) имеет на промежутке первообразную F(x), то и все функции вида F(x)+C будут для нее первообразными на том же промежутке. Обратно, любая первообразная Ф(x) для функции y = f(x) может быть представлена в виде Ф(x) = F(x)+C, где F(x) - одна из первообразных функций, а C - произвольная постоянная.
Доказательство:
По определению первообразной имеем F’(x) = f(x). Учитывая, что производная постоянной равна нулю, получаем
(F(x)+C)’ = F’(x)+C’ = F’(x) = f(x). Это и означает, что F(x)+C является первообразной для y = f(x).Покажем теперь, что если функция y = f(x) задана на некотором промежутке и F(x) - одна из ее первообразных, то Ф(x) может быть представлена в виде
В самом деле, по определению первообразной имеем
Ф’(x) = F(x)+C и F’(x) = f(x).
Но две функции, имеющие на промежутке равные производные, отличаются друг от друга лишь на постоянное слагаемое. Значит, Ф(x) = F(x)+C, что и требовалось доказать.
Определение.
Совокупность всех первообразных для функции y = f(x) на заданном промежутке называется неопределенным интегралом этой функции и обозначается ∫f(x)dx = F(x)+C
Функция f(x) называется подынтегральной функцией, а произведение f(x)*dx - подынтегральным выражением.
Часто говорят: "взять неопределенный интеграл" или "вычислить неопределенный интеграл", понимая под этим следующее: найти множество всех первообразных для подынтегральной функции,
Свойства неопределенного интеграла
1. (f(x)dx) = f(x)
2. ∫f′(x)dx = f(x) + c
3. ∫a ⋅ f(x)dx = a∫f(x)dx, a ≠ 0
4. ∫(f1(x) + f2(x))dx = ∫f1(x)dx + ∫f2(x)dx
Таблица интегралов
Интегрирование подстановкой и по частям в неопределенном интеграле.
Метод интегрирования подстановкой
заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводащимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует.
Пусть тpебyетcя вычислить интеграл ∫f(x)dx. Сделаем подстановку х =φ(t), где φ(t) - функция, имеющая непрерывную производную. Тогда dx=φ"(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй ∫f(x)dx = ∫f(φ(t)) * φ’(t)dt Эта формула также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Метод интегрирования по частям
Пусть u=u(х) и ν=v(х) - функции, имеющие непрерывные производные. Тогда d(uv)=u dv+v du.
Интегрируя это равенство, получим ∫d(uv) = ∫udv + ∫vdu или
∫udv =uv - ∫vdu
Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла ∫udv к вычислению интеграла ∫vdu, который может оказаться существенно более простым, чем исходный.
Что такое интегрирование по частям? Чтобы освоить этот вид интегрирования, давайте для начала вспомним производную произведения:
${{\left(f\cdot g \right)}^{\prime }}={f}"\cdot g+f\cdot {g}"$
Спрашивается: ну и при чем тут интегралы? А давайте теперь проинтегрируем обе стороны этого уравнения. Так и запишем:
$\int{{{\left(f\cdot g \right)}^{\prime }}\text{d}x=}\int{{f}"\cdot g\,\text{d}x+\int{f\cdot {g}"\,\text{d}x}}$
Но что такое первообразная от штриха? Это просто сама функция, которая стоит внутри штриха. Так и запишем:
$f\cdot g=\int{{f}"\cdot g\,\text{d}x+\int{f\cdot {g}"\,\text{d}x}}$
В данном уравнении предлагаю выразить слагаемое. Имеем:
$\int{{f}"\cdot g\,\text{d}x=f\cdot g-\int{f\cdot {g}"\,\text{d}x}}$
Это и есть формула интегрирования по частям
. Таким образом, мы, по сути, меняем местами производную и функцию. Если изначально у нас был интеграл от штриха, умноженной на что-либо, то затем получается интеграл от нового чего-либо, умноженной на штрих. Вот и все правило. На первый взгляд данная формула может показаться сложной и бессмысленной, но, на самом деле, она может значительно упрощать вычисления. Сейчас посмотрим.
Примеры вычисления интегралов
Задача 1. Вычислите:
\[\int{\ln x\,\text{d}x}\]\[\]
Перепишем выражение, добавив перед логарифмом 1:
\[\int{\ln x\,\text{d}x}=\int{1\cdot \ln x\,\text{d}x}\]
Мы имеем право сделать это, потому что ни число, ни функция не изменятся. Теперь сравним это выражение с тем, что у нас написано в формуле. В роли ${f}"$ выступает 1, так и запишем:
$\begin{align}& {f}"=1\Rightarrow f=x \\& g=\ln x\Rightarrow {g}"=\frac{1}{x} \\\end{align}$
Все эти функции есть в таблицах. Теперь, когда мы расписали все элементы, которые входят в наше выражение, перепишем данный интеграл по формуле интегрирования по частям:
\[\begin{align}& \int{1\cdot \ln x\,\text{d}x}=x\ln x-\int{x\cdot \frac{1}{x}\text{d}x}=x\ln x-\int{\text{d}x}= \\& =x\ln x-x+C=x\left(\ln x-1 \right)+C \\\end{align}\]
Все, интеграл найден.
Задача 2. Вычислите:
$\int{x{{\text{e}}^{-x}}\,\text{d}x=\int{x\cdot {{e}^{-x}}\,\text{d}x}}$
Если в роли производной, от которой нам нужно будет сейчас найти первообразную, мы возьмем $x$, то получим${{x}^{2}}$, и итоговое выражение будет содержать ${{x}^{2}}{{\text{e}}^{-x}}$.
Очевидно, задача не упрощается, поэтому мы поменяем местами множители под знаком интеграла:
$\int{x\cdot {{\text{e}}^{-x}}\,\text{d}x}=\int{{{\text{e}}^{-x}}\cdot x\,\text{d}x}$
А вот теперь вводим обозначения:
${f}"={{\text{e}}^{-x}}\Rightarrow f=\int{{{\text{e}}^{-x}}\,\text{d}x}=-{{\text{e}}^{-x}}$
Дифференцируем ${{\text{e}}^{-x}}$:
${{\left({{\text{e}}^{-x}} \right)}^{\prime }}={{\text{e}}^{-x}}\cdot {{\left(-x \right)}^{\prime }}=-{{\text{e}}^{-x}}$
Другими словами, сначала добавляется «минус», а затем обе стороны интегрируются:
\[\begin{align}& {{\left({{\text{e}}^{-x}} \right)}^{\prime }}=-{{\text{e}}^{-x}}\Rightarrow {{\text{e}}^{-x}}=-{{\left({{\text{e}}^{-x}} \right)}^{\prime }} \\& \int{{{\text{e}}^{-x}}\,\text{d}x}=-\int{{{\left({{\text{e}}^{-x}} \right)}^{\prime }}\text{d}x}=-{{\text{e}}^{-x}}+C \\\end{align}\]
Теперь разберёмся с функцией$g$:
$g=x\Rightarrow {g}"=1$
Считаем интеграл:
$\begin{align}& \int{{{\text{e}}^{-x}}\cdot x\,\text{d}x}=x\cdot \left(-{{\text{e}}^{-x}} \right)-\int{\left(-{{\text{e}}^{-x}} \right)\cdot 1\cdot \text{d}x}= \\& =-x{{\text{e}}^{-x}}+\int{{{\text{e}}^{-x}}\,\text{d}x}=-x{{\text{e}}^{-x}}-{{\text{e}}^{-x}}+C=-{{\text{e}}^{-x}}\left(x+1 \right)+C \\\end{align}$
Итак, мы выполнили второе интегрирование по частям.
Задача 3. Вычислите:
$\int{x\cos 3x\,\text{d}x}$
Что в этом случае брать за${f}"$ , а что за$g$? Если в роли производной будет выступать$x$ , то при интегрировании возникнет$\frac{{{x}^{2}}}{2}$, и никуда у нас первый множитель не пропадет — будет $\frac{{{x}^{2}}}{2}\cdot \cos 3x$. Поэтому опять поменяем множители местами:
$\begin{align}& \int{x\cos 3x\,\text{d}x}=\int{\cos 3x\cdot x\,\text{d}x} \\& {f}"=\cos 3x\Rightarrow f=\int{\cos 3x\,\text{d}x}=\frac{\sin 3x}{3} \\& g=x\Rightarrow {g}"=1 \\\end{align}$
Переписываем наше исходное выражение и раскладываем его по формуле интегрирования по частям:
\[\begin{align}& \int{\cos 3x\cdot x\ \text{d}x}=\frac{\sin 3x}{3}\cdot x-\int{\frac{\sin 3x}{3}\text{d}x}= \\& =\frac{x\sin 3x}{3}-\frac{1}{3}\int{\sin 3x\,\text{d}x}=\frac{x\sin 3x}{3}+\frac{\cos 3x}{9}+C \\\end{align}\]
Все, третья задача решена.
В заключение еще раз взглянем на формулу интегрирования по частям
. Как мы выбираем, какой из множителей будет производной, а какой будет настоящей функцией? Критерий здесь всего один: элемент, который мы будем дифференцировать, должен давать либо «красивое» выражение, которое потом сократится, либо при дифференцировании вообще исчезать. На этом урок закончен.
Решение интегралов - задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл... Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы? Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать интегралы и почему без этого никак нельзя обойтись.
Изучаем понятие "интеграл"
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон
и Лейбниц
, но суть вещей не изменилась. Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x)
.
Неопределенным интегралом функции f(x)
называется такая функция F(x)
, производная которой равна функции f(x)
.
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями:
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции. Как найти площадь фигуры, ограниченной графиком функции?
С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
Бари Алибасов и группа "Интеграл"
Кстати!
Для наших читателей сейчас действует скидка 10% на
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решать неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых
точках a
, b
и с
:
Мы уже выяснили, что определенный интеграл - это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим несколько примеров нахождения неопределенных интегралов. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
