Разделы сайта
Выбор редакции:
- Крейсер "красный крым" черноморского флота
- «31 спорный вопрос» русской истории: житие императора Николая II
- Лечебные свойства корня лопуха и его широкое применение в домашних условиях
- Природные ресурсы западной сибири
- Совместимость петуха и змеи в любовных отношениях и браке Он петух она змея совместимость
- Чемерица черная: прекрасная и опасная Противопоказания и побочные действия
- Чем интересна Свято-Михайло-Афонская Закубанская пустынь?
- Порционная сельдь под шубой на праздничный стол
- К чему снится шить во сне
- Примета — разбить зеркало случайно: что делать, если оно треснуло
Реклама
| Первообразная синус в квадрате. Сложные интегралы. Интеграл произведения степеней синуса и косинуса одного и того же аргумента |
Интегралы от тригонометрических функций. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблица первообразных ("интегралов"). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). |
|
|
Интеграл степенной функции. |
Интеграл степенной функции. |
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
|
Интеграл экспоненты, где a-постоянное число. |
|
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
Интеграл, равняющийся натуральному логорифму. |
Интеграл: "Длинный логарифм". |
|
Интеграл: "Длинный логарифм". |
|
|
Интеграл: "Высокий логарифм". |
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму. |
|
Интеграл: "Высокий логарифм". |
|
|
Интеграл косинуса. |
Интеграл синуса. |
|
Интеграл, равный тангенсу. |
Интеграл, равный котангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу |
|
|
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
Интеграл равный косекансу. |
Интеграл, равный секансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
|
|
|
|
Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
Формулы интегрирования по частям. Правила интегрирования.
|
Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. |
|
|
Интегрирование произведения (функции) на постоянную: |
|
|
Интегрирование суммы функций: |
|
|
неопределенные интегралы: |
|
|
Формула интегрирования по частям определенные интегралы: |
|
|
Формула Ньютона-Лейбница определенные интегралы: |
Где F(a),F(b)-значения первообразных в точках b и a соответственно. |
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x - независимая переменная, то:
|
Таблица производных. Табличные производные."таблица производный"-да, к сожалению, именно так их и ищут в интернете |
|
|
Производная степенной функции |
|
|
|
Производная экспоненты |
|
|
Производная экспоненциальной функции |
|
Производная логарифмической функции |
|
|
Производная натурального логарифма функции |
|
|
|
|
|
Производная косеканса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная арккотангенса |
|
|
|
|
|
Производная арккосеканса |
|
|
|
|
|
|
|
|
|
|
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. |
|
|
Производная произведения (функции) на постоянную: |
|
|
Производная суммы (функций): |
|
|
Производная произведения (функций): |
|
|
Производная частного (функций): |
|
|
Производная сложной функции: |
|
Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
|
|
|
|
|
|
|
|
|
|
|
Основное логарифмическое тождество |
|
|
Покажем как можно любую функцию вида a b сделать экспоненциальной. Поскольку функция вида е х называется экспоненциальной, то |
|
|
Любая функция вида a b может быть представлена в виде степени десяти |
|
Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045…) ln(e)=1; ln(1)=0
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:

При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1)
,
где f(x) - функция, имеющая при х=а производные
всех порядков. R n
- остаточный член в ряде Тейлора
определяется выражением

2)
k-тый коэффициент (при х k) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при
a=0

члены ряда определяются по формуле

Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации (приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis - линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена(=Макларена, Тейлора в окрестностях точки 0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
|
|
|
|
|
|
Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений , где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям . То есть, в одном примере комбинируются сразу два приёма . И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе . Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от сложных дробей , которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций . В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки .
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала .
(4) Берём оставшиеся интегралы. Обратите внимание, что в логарифме можно использовать скобки, а не модуль, так как .
(5) Проводим обратную замену, выразив из прямой замены «тэ»:
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Пример 2
Найти неопределенный интеграл
Пример 3
Найти неопределенный интеграл
Пример 4
Найти неопределенный интеграл
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений, думаю, очевидно. Почему я подобрал однотипные примеры? Часто встречаются в своем амплуа. Чаще, пожалуй, только что-нибудь вроде ![]() .
.
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Методом сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра:
Пример 5
Найти неопределенный интеграл
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе не сложно. Если знаешь как.
Обозначим рассматриваемый интеграл латинской буквой и начнем решение:![]()
Интегрируем по частям:

(1) Готовим подынтегральную функцию для почленного деления.
(2) Почленно делим подынтегральную функцию. Возможно, не всем понятно, распишу подробнее:
(3) Используем свойство линейности неопределенного интеграла.
(4) Берём последний интеграл («длинный» логарифм).
Теперь смотрим на самое начало решения:
И на концовку:
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе!
Приравниваем начало и конец:![]()
Переносим в левую часть со сменой знака:![]()
А двойку сносим в правую часть. В результате:![]()
Константу , строго говоря, надо было добавить ранее, но приписал её в конце. Настоятельно рекомендую прочитать, в чём тут строгость:
Примечание:
Более строго заключительный этап решения выглядит так:
Таким образом:

Константу можно переобозначить через . Почему можно переобозначить? Потому что всё равно принимает любые
значения, и в этом смысле между константами и нет никакой разницы.
В результате:
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях . И там я буду строг. А здесь такая вольность допускается мной только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования.
Пример 6
Найти неопределенный интеграл
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, то решение в любом случае сводится к двум разобранным примерам.
Например, рассмотрим интеграл ![]() . Всё, что нужно сделать – предварительно выделить полный квадрат
:
. Всё, что нужно сделать – предварительно выделить полный квадрат
:
.
Далее проводится линейная замена, которая обходится «без всяких последствий»:
, в результате чего получается интеграл . Нечто знакомое, правда?
Или такой пример, с квадратным двучленом:
Выделяем полный квадрат:
И, после линейной замены , получаем интеграл , который также решается по уже рассмотренному алгоритму.
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе:
– интеграл от экспоненты, умноженной на синус;
– интеграл от экспоненты, умноженной на косинус.
В перечисленных интегралах по частям придется интегрировать уже два раза:
Пример 7
Найти неопределенный интеграл
Подынтегральная функция – экспонента, умноженная на синус.
Дважды интегрируем по частям и сводим интеграл к себе:![]()



В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
Переносим в левую часть со сменой знака и выражаем наш интеграл:
Готово. Попутно желательно причесать правую часть, т.е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:![]()
За мы обозначили экспоненту. Возникает вопрос, именно экспоненту всегда нужно обозначать за ? Не обязательно. На самом деле в рассмотренном интеграле принципиально
без разницы
, что обозначать за , можно было пойти другим путём:
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании).
То есть, за можно обозначить и тригонометрическую функцию. Но, в рассмотренном примере это менее рационально, поскольку появятся дроби. При желании можете попытаться решить данный пример вторым способом, ответы обязательно должны совпасть.
Пример 8
Найти неопределенный интеграл
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за , экспоненту или тригонометрическую функцию? Полное решение и ответ в конце урока.
И, конечно, не забывайте, что большинство ответов данного урока достаточно легко проверить дифференцированием!
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например: . Попутаться в подобном интеграле придется многим, частенько путаюсь и я сам. Дело в том, что в решении велика вероятность появления дробей, и очень просто что-нибудь по невнимательности потерять. Кроме того, велика вероятность ошибки в знаках, обратите внимание, что в показателе экспоненты есть знак «минус», и это вносит дополнительную трудность.
На завершающем этапе часто получается примерно следующее:
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Пример 9
Найти неопределенный интеграл
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:![]()
Замена тут проста:![]()
Смотрим на жизнь после замены:
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим из-под корня.
(3) Числитель и знаменатель сокращаем на . Заодно под корнем я переставил слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей
, решается методом выделения полного квадрата
. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально , то обратно: .
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня .
Пример 10
Найти неопределенный интеграл![]()
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же:![]()
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены: ![]()
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Пример 11
Найти неопределенный интеграл
Пример 12
Найти неопределенный интеграл
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом , метод решения которого рассматривался на уроке Интегралы от иррациональных функций .
Интеграл от неразложимого многочлена 2-й степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Пример 13
Найти неопределенный интеграл
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:
Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:

Для интеграла вида ( – натуральное число) выведена рекуррентная
формула понижения степени:
, где ![]() – интеграл степенью ниже.
– интеграл степенью ниже.
Убедимся в справедливости данной формулы для прорешанного интеграла .
В данном случае: , , используем формулу:
Как видите, ответы совпадают.
Пример 14
Найти неопределенный интеграл
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители
квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу , поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции , пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Интегрирование сложных тригонометрических функций
Прилагательное «сложный» для большинства примеров вновь носит во многом условный характер. Начнем с тангенсов и котангенсов в высоких степенях. С точки зрения используемых методов решения тангенс и котангенс – почти одно и тоже, поэтому я больше буду говорить о тангенсе, подразумевая, что продемонстрированный прием решения интеграла справедлив и для котангенса тоже.
На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать!
Рассмотрим еще один канонический пример, интеграл от единицы, деленной на синус:
Пример 17
Найти неопределенный интеграл
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Я приведу полное решение с комментами к каждому шагу:

(1) Используем тригонометрическую формулу синуса двойного угла .
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на .
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пара простых примеров для самостоятельного решения:
Пример 18
Найти неопределенный интеграл
Указание: Самым первым действием следует использовать формулу приведения ![]() и аккуратно провести аналогичные предыдущему примеру действия.
и аккуратно провести аналогичные предыдущему примеру действия.
Пример 19
Найти неопределенный интеграл
Ну, это совсем простой пример.
Полные решения и ответы в конце урока.
Думаю, теперь ни у кого не возникнет проблем с интегралами:![]() и т.п.
и т.п.
В чём состоит идея метода? Идея состоит в том, чтобы с помощью преобразований, тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса . То есть, речь идет о замене: ![]() . В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала .
. В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала .
Аналогичные рассуждения, как я уже оговаривался, можно провести для котангенса.
Существует и формальная предпосылка для применения вышеуказанной замены:
Сумма степеней косинуса и синуса – целое отрицательное ЧЁТНОЕ число , например:
для интеграла – целое отрицательное ЧЁТНОЕ число.
! Примечание :если подынтегральная функция содержит ТОЛЬКО синус или ТОЛЬКО косинус, то интеграл берётся и при отрицательной нечётной степени (простейшие случаи – в Примерах №№17, 18).
Рассмотрим пару более содержательных заданий на это правило:
Пример 20
Найти неопределенный интеграл
Сумма степеней синуса и косинуса : 2 – 6 = –4 – целое отрицательное ЧЁТНОЕ число, значит, интеграл можно свести к тангенсам и его производной:
(1) Преобразуем знаменатель.
(2) По известной формуле получаем .
(3) Преобразуем знаменатель.
(4) Используем формулу ![]() .
.
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену . Более опытные студенты замену могут и не проводить, но все-таки лучше заменить тангенс одной буквой – меньше риск запутаться.
Пример 21
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Держитесь, начинаются чемпионские раунды =)
Зачастую в подынтегральной функции находится «солянка»:
Пример 22
Найти неопределенный интеграл![]()
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:

Искусственное преобразование в самом начале и остальные шаги оставлю без комментариев, поскольку обо всем уже говорилось выше.
Пара творческих примеров для самостоятельного решения:
Пример 23
Найти неопределенный интеграл![]()
Пример 24
Найти неопределенный интеграл![]()
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока
| Читайте: |
|---|
Новое
- «31 спорный вопрос» русской истории: житие императора Николая II
- Лечебные свойства корня лопуха и его широкое применение в домашних условиях
- Природные ресурсы западной сибири
- Совместимость петуха и змеи в любовных отношениях и браке Он петух она змея совместимость
- Чемерица черная: прекрасная и опасная Противопоказания и побочные действия
- Чем интересна Свято-Михайло-Афонская Закубанская пустынь?
- Порционная сельдь под шубой на праздничный стол
- К чему снится шить во сне
- Примета — разбить зеркало случайно: что делать, если оно треснуло
- Самостоятельные заговоры на удачу и деньги









 ,
, 



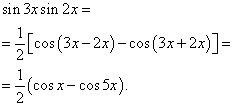

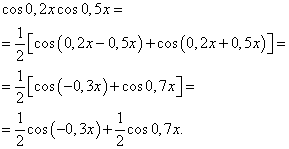
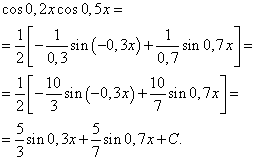



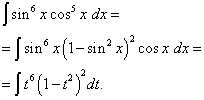

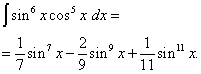

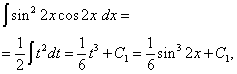

 .
.







 Производная
Производная

 Производная
секанса
Производная
секанса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
тангенса
Производная
тангенса Производная
котангенса
Производная
котангенса Производная
арктангенса
Производная
арктангенса Производная
арккотангенса
Производная
арккотангенса Производная
арктангенса
Производная
арктангенса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
арксеканса
Производная
арксеканса Производная
гиперболического синуса
Производная
гиперболического синуса Производная
гиперболического синуса в английской
версии
Производная
гиперболического синуса в английской
версии Производная
гиперболического косинуса
Производная
гиперболического косинуса Производная
гиперболического косинуса в английской
версии
Производная
гиперболического косинуса в английской
версии Производная
гиперболического тангенса
Производная
гиперболического тангенса Производная
гиперболического котангенса
Производная
гиперболического котангенса Производная
гиперболического секанса
Производная
гиперболического секанса Производная
гиперболического косеканса
Производная
гиперболического косеканса








































